BASEMENT
SVM, SVR 본문
1. SVM (Support Vector Machine)
1. 개념
- 이질적인 두개 또는 그 이상의 데이터 집단을 분류하는 최적의 초평면을 찾는 모델
-> 분류되지 않은 새로운 점이 나타나면 경계의 어느 쪽에 속하는지 확인해서 분류할 수 있음
- 각 데이터 항목을 n차원 공간상 하나의 점으로 표시함
- 분류 또는 회귀문제에 사용할 수 있는 알고리즘
- 딥러닝 못지 않은 성능, 가벼움
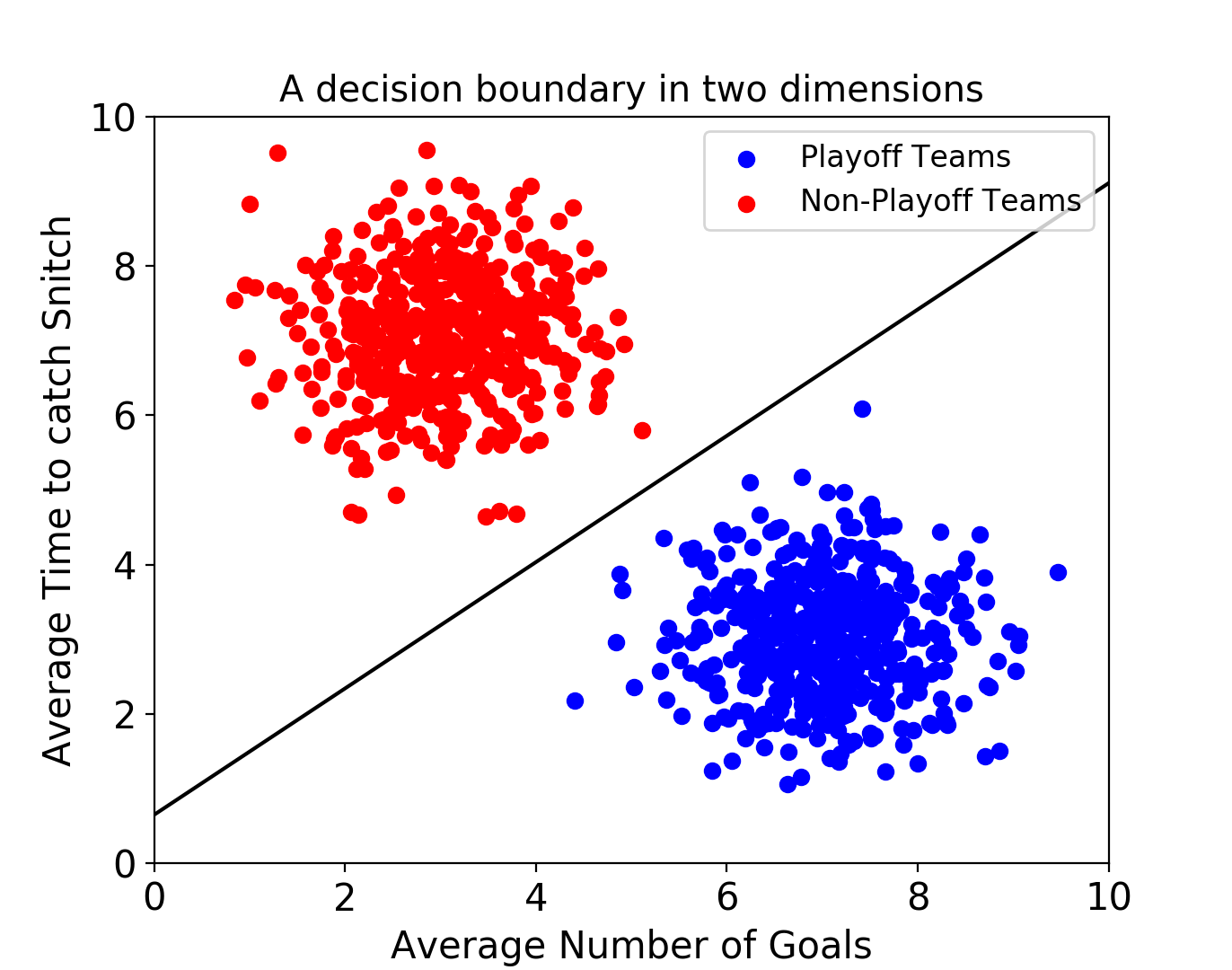
- Classification한 다음 Margin이 가장 큰 선을 찾음
- Margin : 초평면 가까이에 있는 서포트 벡터에서 초평면까지의 거리의 합
- 서포트 벡터 : 두 클래스 사이의 경계에 위치한 데이터 포인트
-> 서포트 벡터들이 결정 경계를 만드는데 영향
2. SVM 분류
- 각각 커널에서는 최적화를 도와주는 파라미터들이 따로 존재함
- 모든 조건을 바꾸며 실험해보면서 최적의 예측률을 보여주는 최적의 파라미터를 찾아야함
1) Hard Margin

- 두 클래스로 확실하게 분류함
- 정제된 데이터에서 사용
- Objective function (목적함수) : 마진을 최대화함
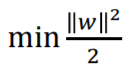
2) Soft Margin

- 오차가 포함됨
- 비선형 분류에서 사용
- 비선형 분류 : 주어진 데이터를 고차원 특징공간으로 사상하는 작업 필요
-> 커널트릭 (Linear Kernel, Polynomial Kernel, RBF 등)을 사용함
- Objective function
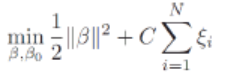
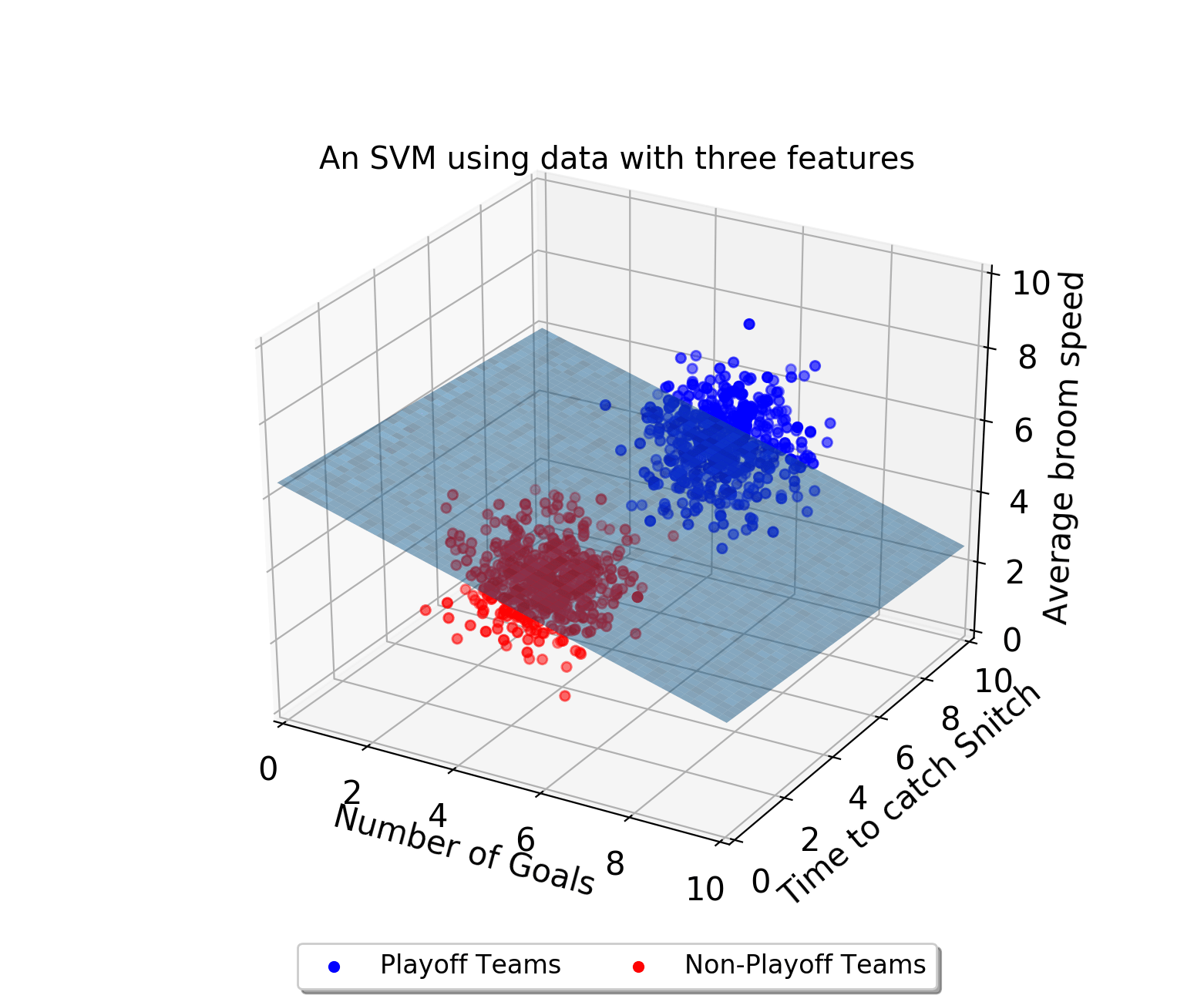
3. SVM 커널트릭

- 비선형 분류에서 사용
- 주어진 데이터를 고차원 데이터로 사상(mapping)하는 것
- 일부 공간에서 점으로 표현
- RBF, Linear kernel, Polynomial kernel 등
4. kernel의 매개변수
1) C (cost)
- 얼마나 많은 데이터 샘플이 다른 클래스에 놓이는 것을 허용하는지 결정함
- 오차를 허용할 수 있는 범위
2) gamma
- 하나의 데이터 샘플이 영향력을 행사하는 거리를 결정함

-> C는 데이터 샘플들이 다른 클래스에 놓이는 것을 허용결정, gamma는 결정경계의 곡률 결정
5. SVM 사용
from sklearn import svm
clf = svm.SVC(kernel='linear')
clf = svm.SVC(kernel='rbf', C=1.0, gamma=0.10)
clf.fit(x_train, y_train)
clf.predict(x_test)
clf.score(x_test, y_test)- kernel : 기본값 rbf -> 주로 rbf, linear, poly 사용
- C : 기본값 1.0 -> 값을 낮추면 초평면이 매끄러워지고, 높이면 서포트벡터들을 더 잘 분류함
- Gamma : 기본값 auto -> 값을 낮추면 초평면에서 멀리 떨어진 서포트벡터들의 영향이 낮고, 높이면 영향이 큼. 값을 높일 경우 초평면이 울퉁불퉁하게 됨
cf) degree : poly kernel일 경우에만 사용. 다항식 커널 함수의 각도
- SVM Overfitting 방지 : 최적 파라미터로 Overfitting 방지
=> Grid Search, 교차검증도로 최적의 파라미터를 찾아야 함
6. SVM 예제
1)
from sklearn.svm import SVC
classifier = SVC(kernel='linear')
training_points = [[1,2],[1,5],[2,2],[7,5],[9,4],[8,2]]
labels = [1,1,1,0,0,0]
classifier.fit(training_points, labels)
print(classifier.predict([[3,2]])-> [3,2]는 클래스 1로 분류됨
2) iris 데이터
from sklearn.datasets import load_iris
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split, cross_val_score
iris = load_iris()
col1 = 0
col2 = 1
X = iris.data[:,:2] # 시각화를 위해 속성 2개만 선정
y = iris.target
# train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
X_train.shape, X_test.shape, y_train.shape, y_test.shape
# 모델 정의
model = SVC()
# 학습시키기
model.fit(X_train, y_train)
# 평가하기
score1 = model.score(X_train, y_train)
print(score1)# 그래프로 확인
import mglearn
plt.figure(figsize=[10,8])
mglearn.plots.plot_2d_classification(model, X_train, cm='summer')
mglearn.discrete_scatter(X_train[:,0], X_train[:,1], y_train)# C (cost) 적용
model = SVC(C=10)
model.fit(X_train, y_train)
score = model.score(X_train, y_train)
display(score)
plt.figure(figsize=[10,8])
mglearn.plots.plot_2d_classification(model, X_train, cm='spring')
mglearn.discrete_scatter(X_train[:,0], X_train[:,1], y_train)# gamma 적용
model = SVC(gamma=10)
model.fit(X_train, y_train)
score = model.score(X_train, y_train)
display(score)
plt.figure(figsize=[10,8])
mglearn.plots.plot_2d_classification(model, X_train, cm='spring')
mglearn.discrete_scatter(X_train[:,0], X_train[:,1], y_train)
3) breast_cancer 데이터
from sklearn.datasets import load_breast_cancer
breast_cancer_data = load_breast_cancer()
X_Data = pd.DataFrame(breast_cancer_data.data)
y = pd.DataFrame(breast_cancer_data.target)from sklearn.svm import SVC
import sklearn.metrics as mt
from sklearn.model_selection import cross_val_score, cross_validate
# SVM, kernel = 'linear'로 선형분리 진행
svm_clf = SVC(kernel='linear')
# 교차 검증
scores = cross_val_score(svm_clf, X_Data, y, cv=5)
scores
print('교차검증 평균: ', scores.mean())
print(pd.DataFrame(cross_validate(svm_clf, X_Data, y, cv=5)))# SVM, kernel = 'rbf'로 비선형분리 진행
svm_clf = SVC(kernel='rbf')
# 교차검증
scores = cross_val_score(svm_clf, X_Data, y, cv=5)
scores
print(pd.DataFrame(cross_validate(svm_clf, X_Data, y, cv=5)))
print('Cross Mean: ', scores.mean())# GridSearch - kernel='linear'
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X_Data, y, test_size=0.3, random_state=42)
# 테스트하고자 하는 파라미터 값들을 사전타입으로 정의함
svm_clf = SVC(kernel='linear', random_state=42)
parameters = {'C':[0.001,0.01,0.1,1,10,25,50,100]}
grid_svm = GridSearchCV(svm_clf, param_grid=parameters, cv=5)
grid_svm.fit(X_train, y_train)
print(grid_svm.best_params_) # 최적 파라미터를 보여줌
print(grid_svm.best_score_)
result = pd.DataFrame(grid_svm.cv_results_['params'])
result['mean_test_score'] = grid_svm.cv_results_['mean_test_score']
result.sort_values(by='mean_test_score', ascending=False)# GridSearch - kernel='rbf'
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X_Data, y, test_size=0.3, random_state=42)
# 테스트하고자 하는 파라미터 값들을 사전타입으로 정의
svm_clf = SVC(kernel='rbf', random_state=42)
parameters = {'C':[0.001,0.01,0.1,1,10,25,50,100],
'gamma':[0.001, 0.01, 0.1, 1, 10, 25, 50, 100]} # gamma 추가
grid_svm = GridSearchCV(svm_clf, param_grid=parameters, cv=5)
grid_svm.fit(X_train, y_train)
print(grid_svm.best_params_)
print(grid_svm.best_score_)
model = grid_svm.best_estimator_ # 최적의 파라미터로 모델 생성
y_pred = model.predict(X_test)
from sklearn import metrics
print("Accuracy: ", metrics.accuracy_score(y_test, y_pred))
result = pd.DataFrame(grid_svm.cv_results_['params'])
result['mean_test_score'] = grid_svm.cv_results_['mean_test_score']
result.sort_values(by='mean_test_score', ascending=False)
2. SVR (Support Vector Regression)
1. 개념
- SVM에 손실함수를 도입하여 회귀식을 구성함
- 손실함수 : ϵ-insensitive, Gaussian 등
- 회귀선 : 오차를 줄이고 정확도를 높임
2. SVR 사용
from sklearn.svm import SVR
svr_rbf = SVR(kernel='rbf', C=100, gamma=0.1, epsilon=.1)
svr_lin = SVR(kernel='linear', C=100, gamma='auto')
svr_poly = SVR(kernel='poly', C=100, gamma=0.1, degree=3, epsilon=.1, coef0=1)
y_rbf = svr_fbf.fit(X,y).predict(X)
y_lin = svr_lin.fit(X,y).predict(X)
y_poly = svr_poly.fit(X,y).predict(X)
3. SVR 예제
1) boston 데이터
from sklearn.svm import SVR
from sklearn.datasets import load_boston
from sklearn.datasets import make_regression
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_val_score
from sklearn.preprocessing import scale
import matplotlib.pyplot as plt
boston = load_boston()
x, y = boston.data, boston.target
# StandardScale
x = scale(x)
y= scale(y)
xtrain, xtest, ytrain, ytest = train_test_split(x, y, test_size=.3)
svr = SVR(kernel='rbf', gamma='auto')
svr.fit(xtrain, ytrain)score = svr.score(xtrain, ytrain)
print("R-squared: ", score)
cv_score = cross_val_score(svr, x, y, cv=5)
print("CV mean score: ", cv_score.mean())
ypred = svr.predict(xtest)
mse = mean_squared_error(ytest, ypred)
print("MSE: ", mse)
x_ax = range(len(ytest))
plt.plot(x_ax, ytest, label='origianl')
plt.plot(x_ax, ypred, label="predicted")
plt.title("Botson test and predicted data")
plt.legend()
plt.show()
-> SVR : 선형 회귀보다 비선형 회귀에 적합함(시계열 데이터 등). 오차가 적고 모델 예측 성능이 높음
'Programming > Machine Learning' 카테고리의 다른 글
| 랜덤포레스트 (Random Forest) (0) | 2020.10.10 |
|---|---|
| 의사결정트리 (0) | 2020.10.10 |
| Naive Bayes (나이브 베이즈) (0) | 2020.10.05 |
| KNN 알고리즘 (0) | 2020.09.27 |
| 모델 성능 평가 척도, ROC 커브 (0) | 2020.09.27 |



